++ 50 ++ 比の性質 比の求め方 493768
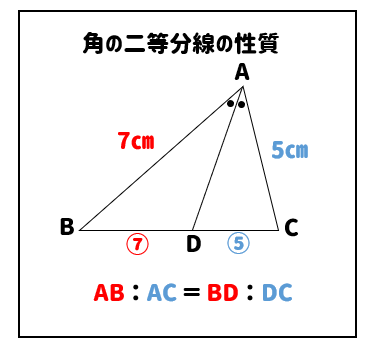
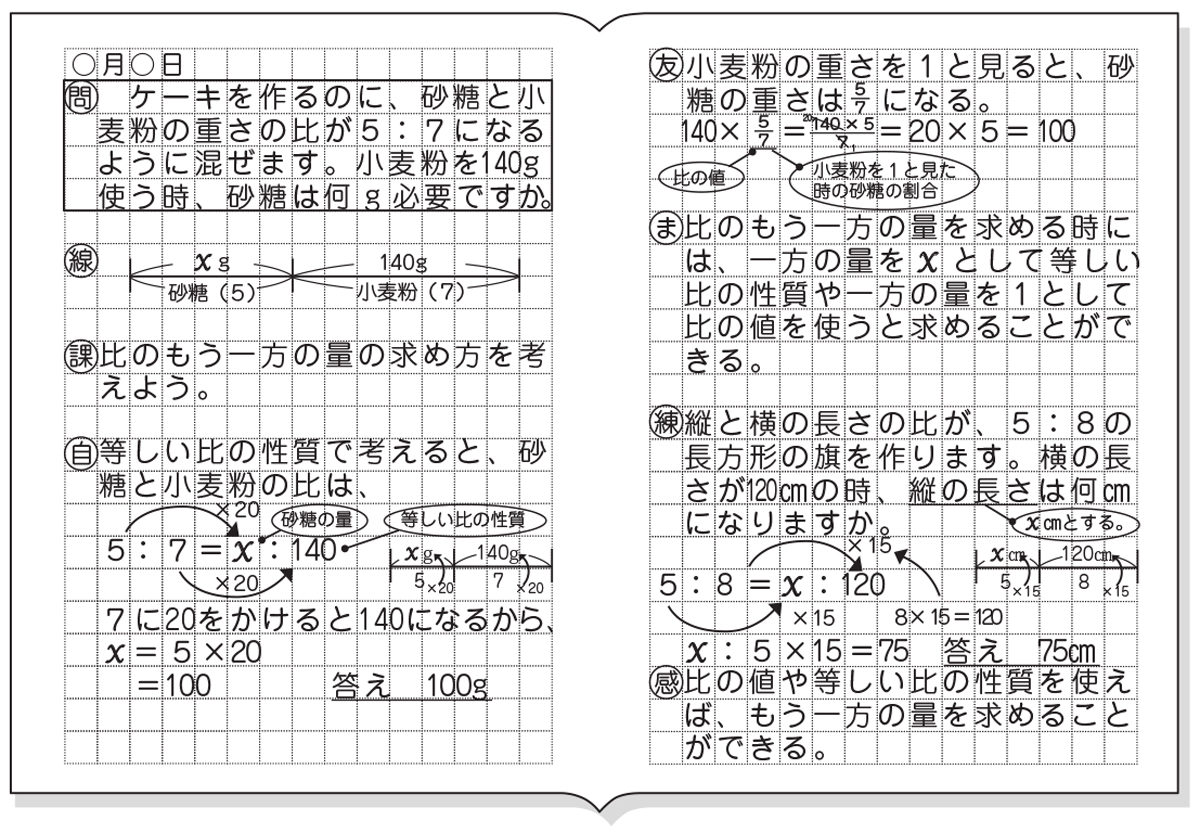
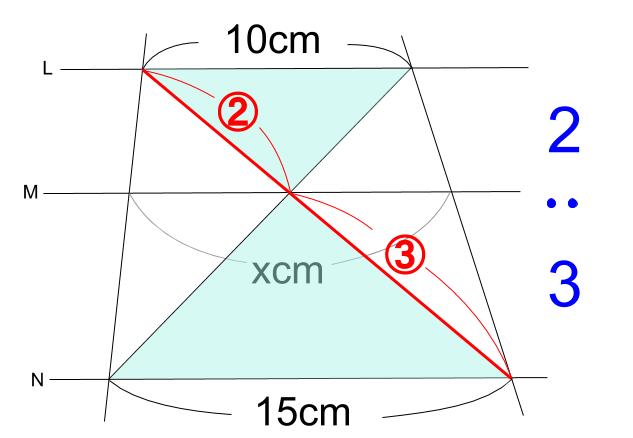
面積比の求め方を理解しよう こちらの記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。 人によっては三角形だと納得しにくいかもしれませんが、例えば正方形であればノートのマス目などを見てわかりやすいと思います。
比の性質 比の求め方- 定義や公式(面積の求め方)、面積比の計算問題 この記事では、「台形」の定義や面積の公式、性質などをできるだけわかりやすく解説していきます。 計算問題も紹介していきますので、この記事を通してぜひマスターしてくださいね! 台形とは相対質量は、基準である炭素の相対質量12に、その原子と炭素との質量の比をかけると求めることができる。 例えば次の問題を見てみよう。 問題 水素( 1 H)の質量は炭素の$\frac{ 1 }{ 12 }$である。このとき、 1 Hの相対
比の性質 比の求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  | |
「比の性質 比の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「比の性質 比の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「比の性質 比の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「比の性質 比の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「比の性質 比の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「比の性質 比の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
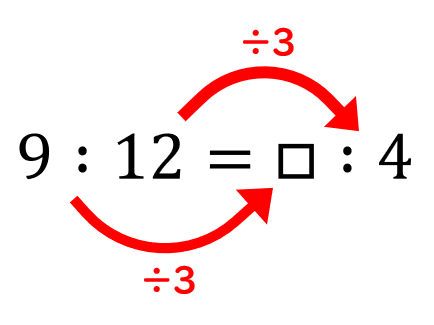 |  | |
 | ||
「比の性質 比の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「比の性質 比の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |
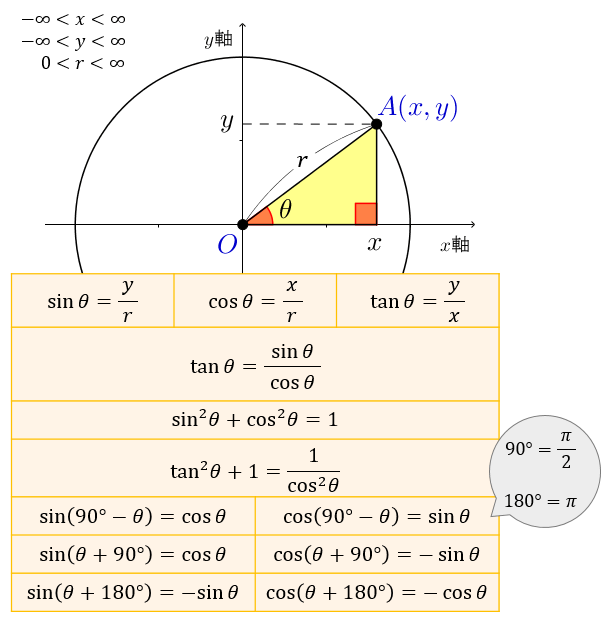
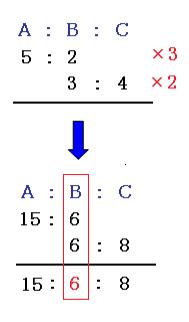
直角三角形の辺の比 のことをいいます。 直角 三角 形の辺の 比 、省略して 三角比 ! と覚えておけばよいね (^^) 結論を最初に書いておくと、こんな感じです。 斜辺と対辺の比をとって、分数の形で表した値を (正弦)といいます。 斜辺と底辺の比をとって、分数の形で表した値を (余弦)といいます。 底辺と対辺の比をとって、分数の形で表した値を (正接比は、その比に同じ数を掛けるか割った別の比と同じという性質を持っています。 12 = 24(左の比に2を掛けたのが右の比) 36 = 12(左の比を3で割ったのが右の比)
コメント
コメントを投稿