√画像をダウンロード 三��形の比の定理 ポイント 287441-三角形の比の定理 ポイ���ト
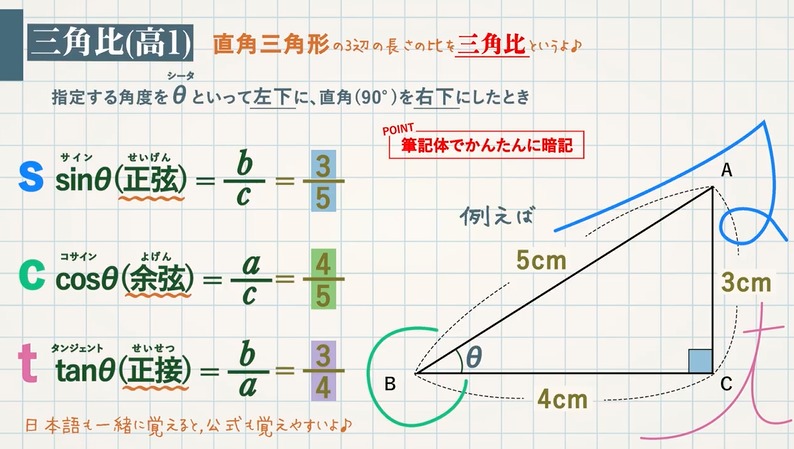
1 三角比は直角三角形から得られる値 11 三角比は直角三角形の2辺の関係を表す値 12 三角比は実は中学でも使っていた 13 1つの鋭角が決まると、三角比も決まる 2 相似の関係にある直角三角形の三角比
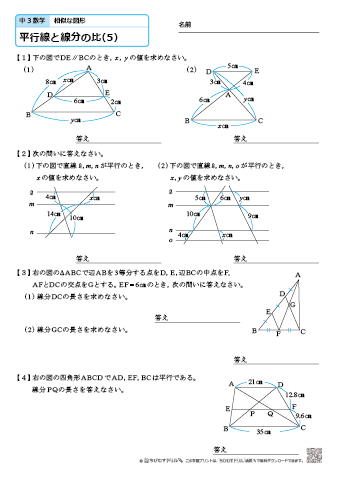
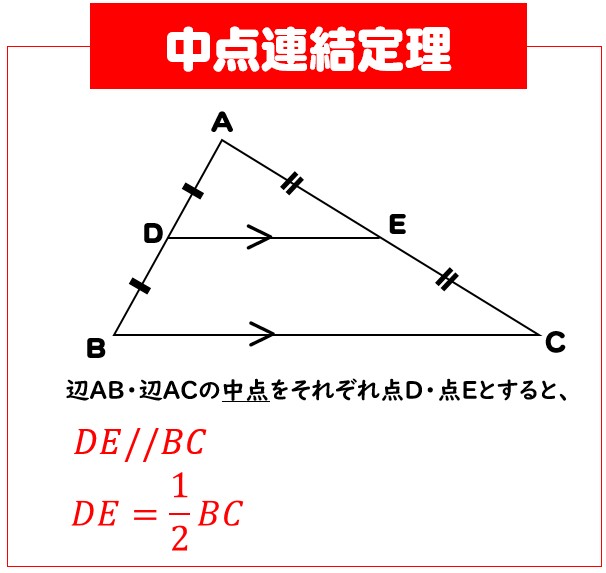
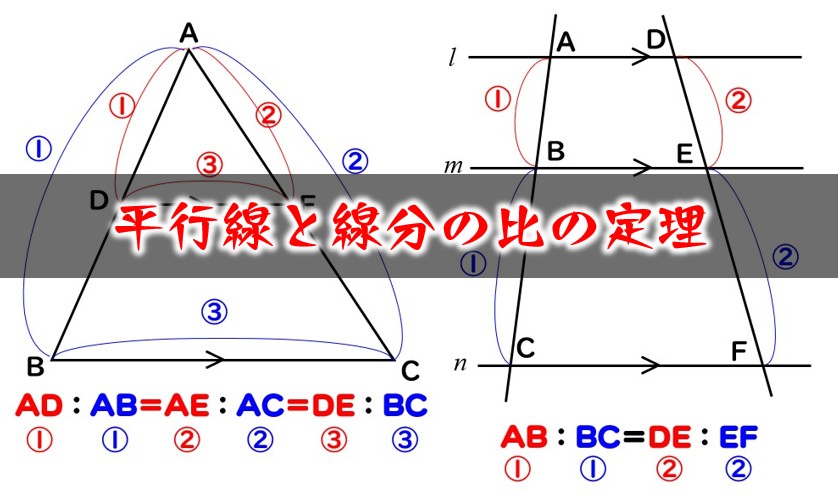
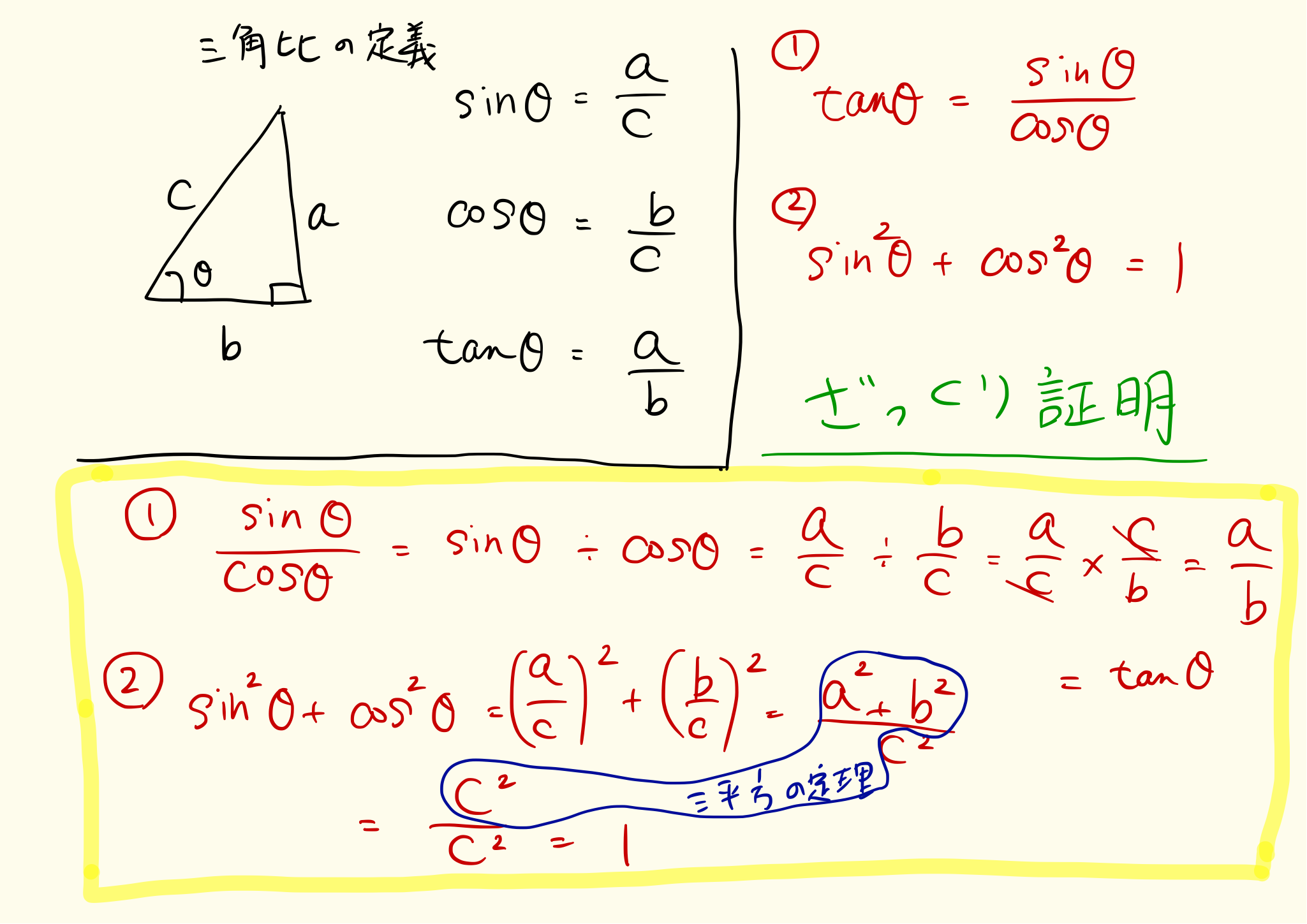
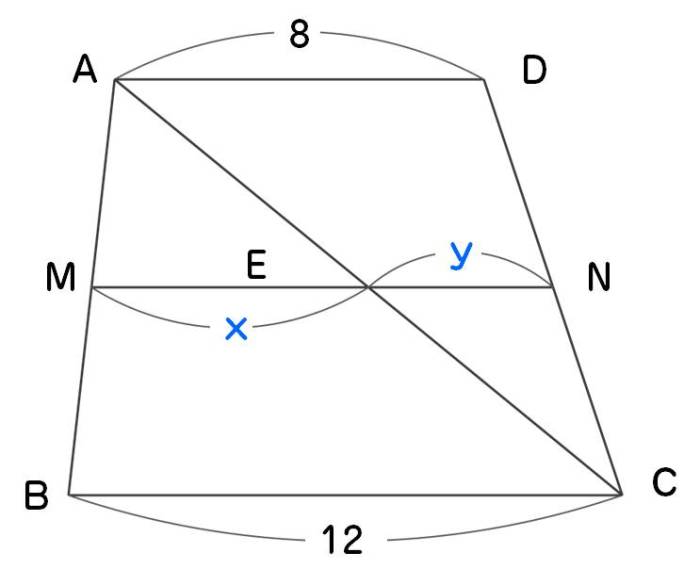
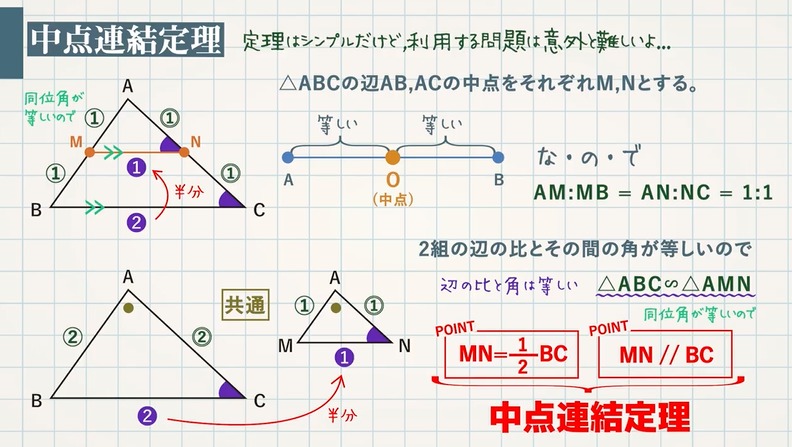
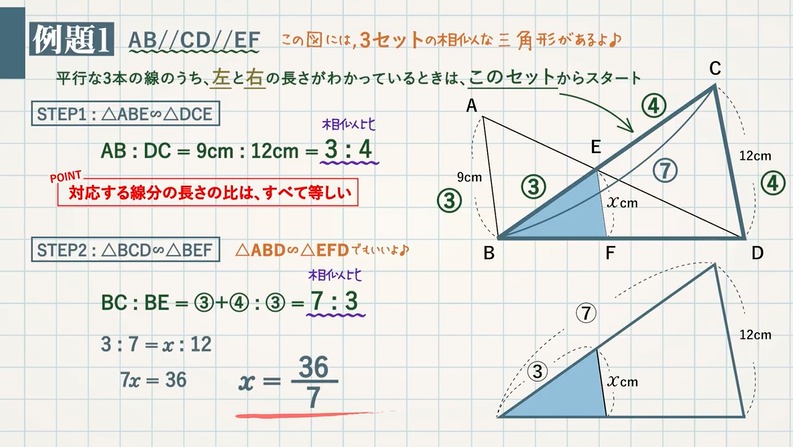
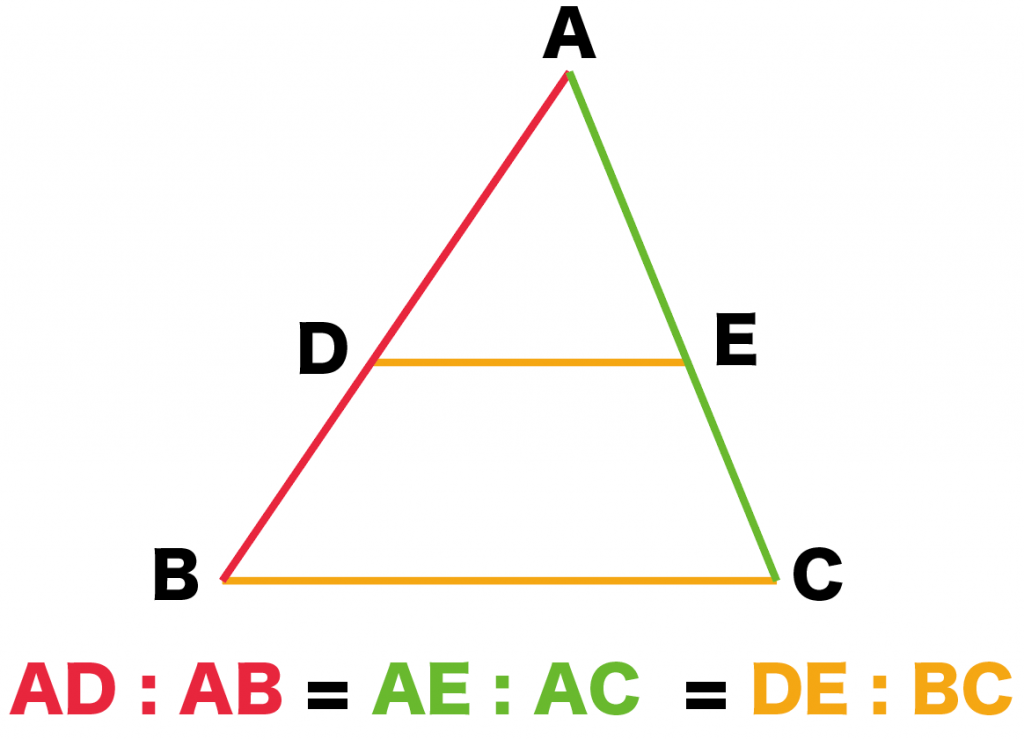
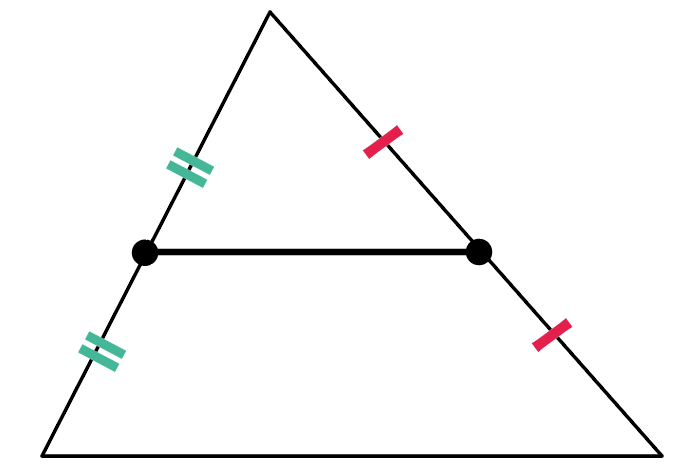
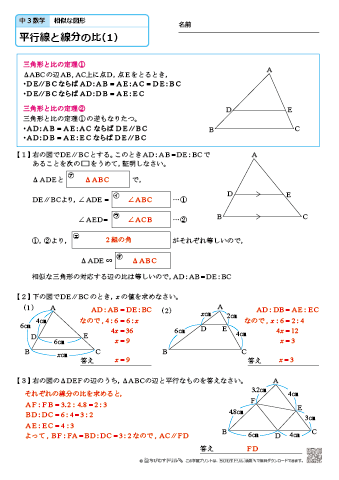
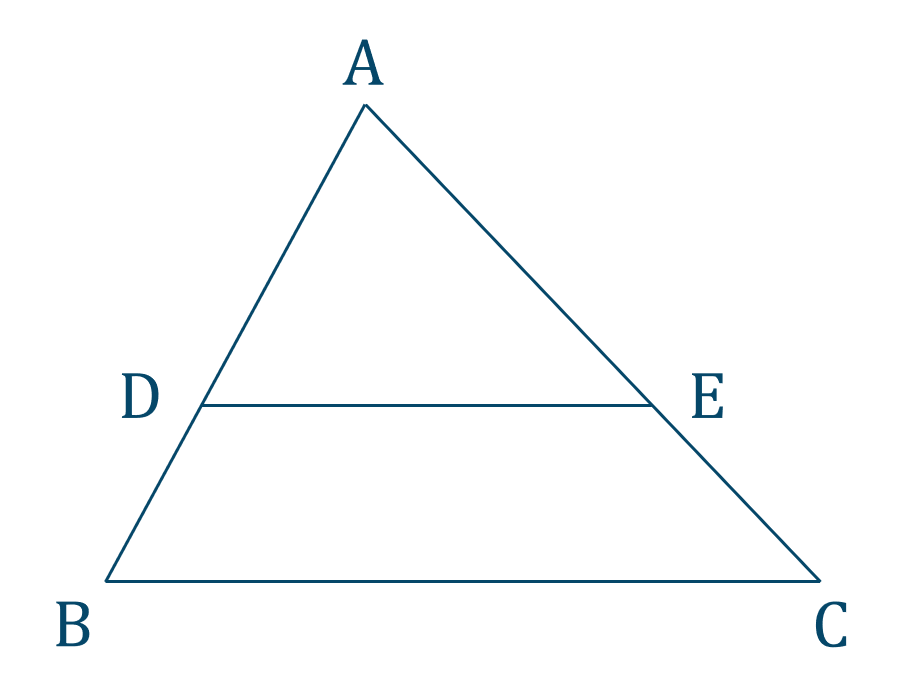
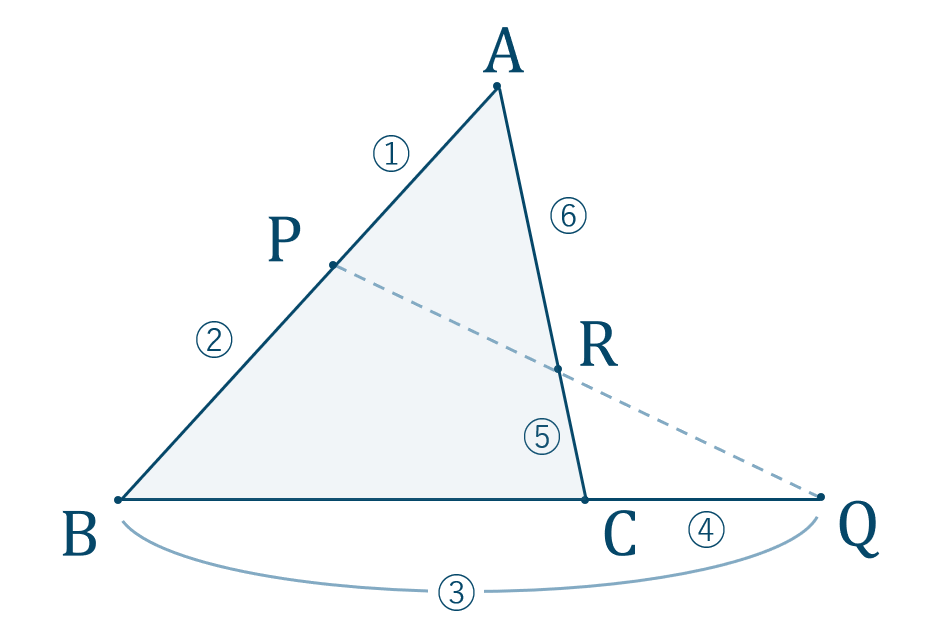
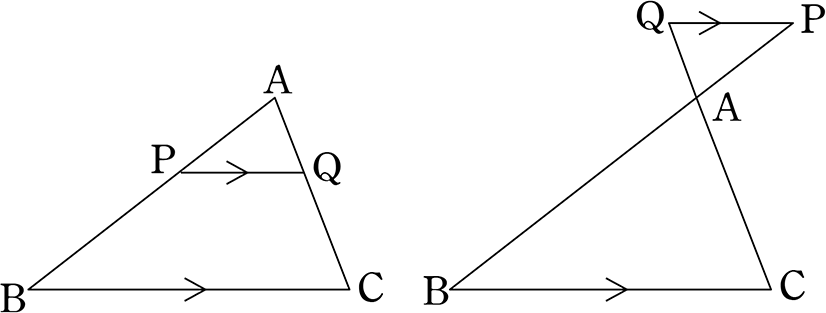
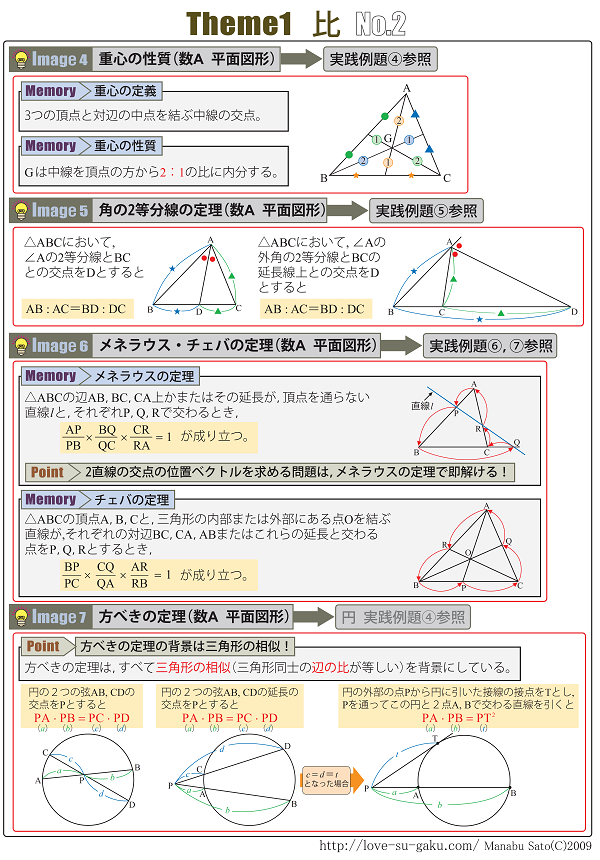
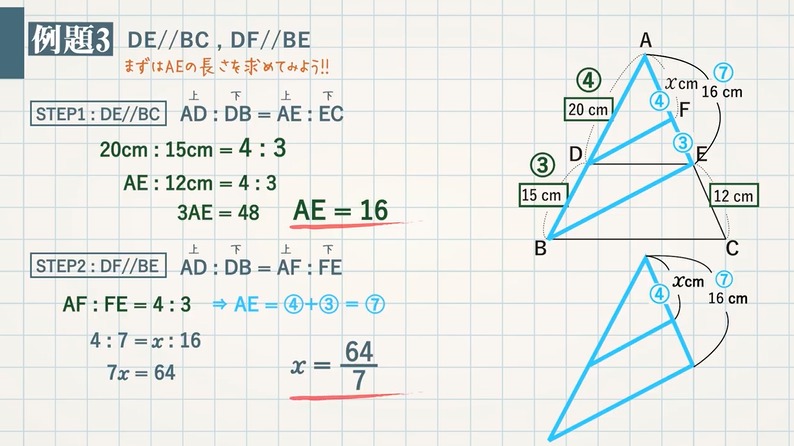
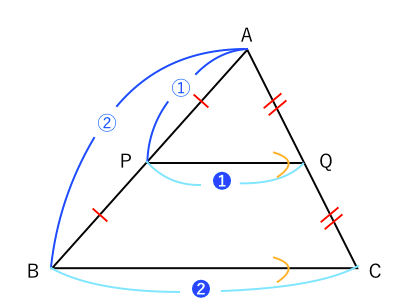
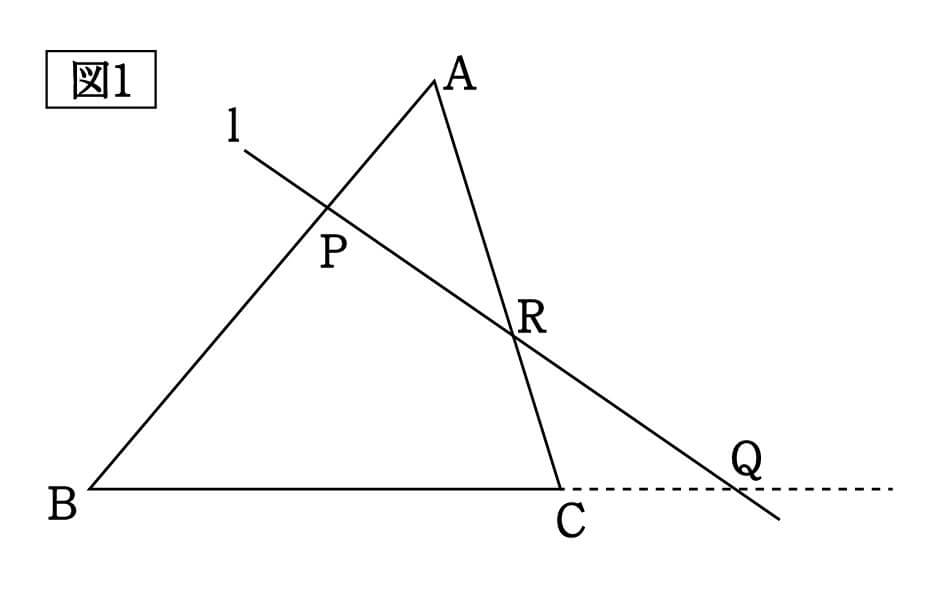
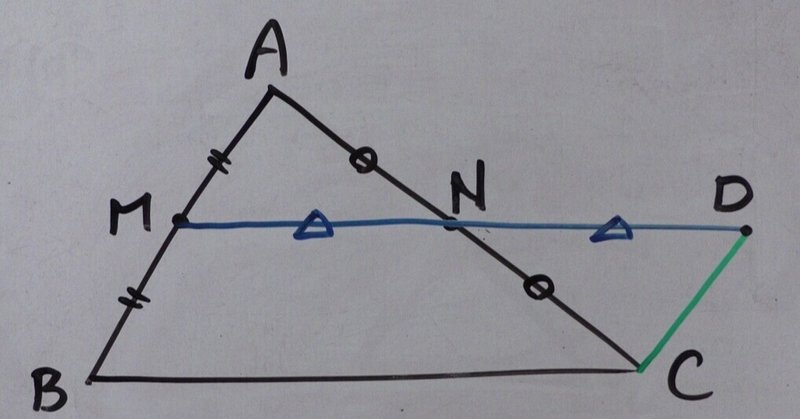
三角形の比の定理 ポイント- 三角比とは? 定義の意味やポイントについて 発想の原点は"相似"にあり "合同・相似"を深く知れば、三角比や正弦定理・余弦定理の理解も深くなる で、 "三角形の辺や角の大きさといった条件をいくつか与えると、その条件をみたす三角形がただ三角形と比の定理 A B C D E ABCの辺AB,AC上の点をそれぞれD, Eとするとき、 ①DE//BCならADAB=AEAC=DEBCである。 ②DE//BCならADDB=AEECである。 ※この定理はD, Eが辺BA, CAの延長上にあっても成り立つ。 定理の証明 例それぞれBC//DEである。 8cm 6cm 9cm 7cm x y A B C D E BC//DEより BCDE=ACAE=ABAD 86=x9 6x=72 x=12 86=7y 8y=42 y= 21 4 A B C D E 6cm
三角形の比の定理 ポイントのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三角形の比の定理 ポイント」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「三角形の比の定理 ポイント」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三角形の比の定理 ポイント」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「三角形の比の定理 ポイント」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三角形の比の定理 ポイント」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「三角形の比の定理 ポイント」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三角形の比の定理 ポイント」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  |  |
「三角形の比の定理 ポイント」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |
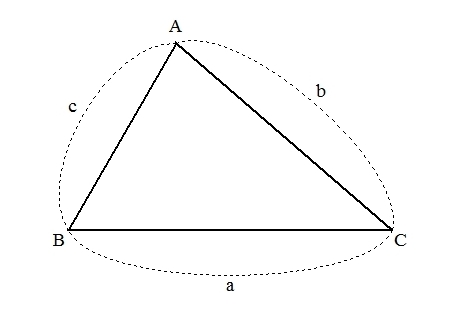
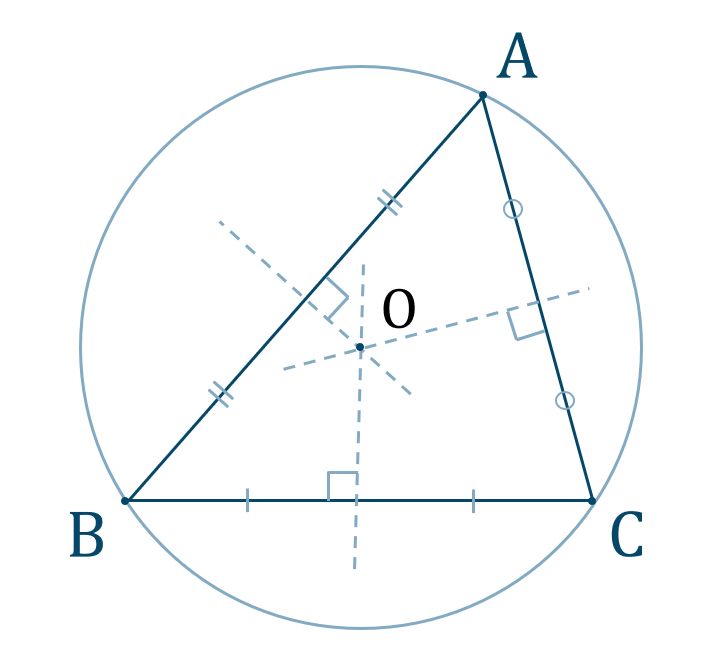
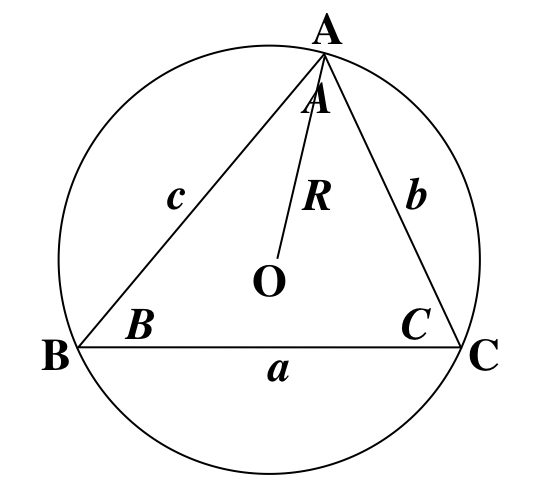
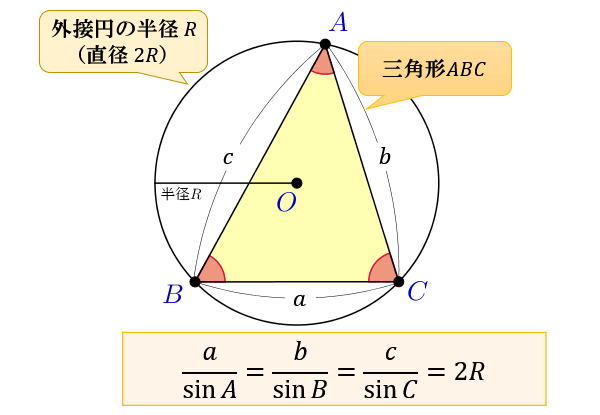
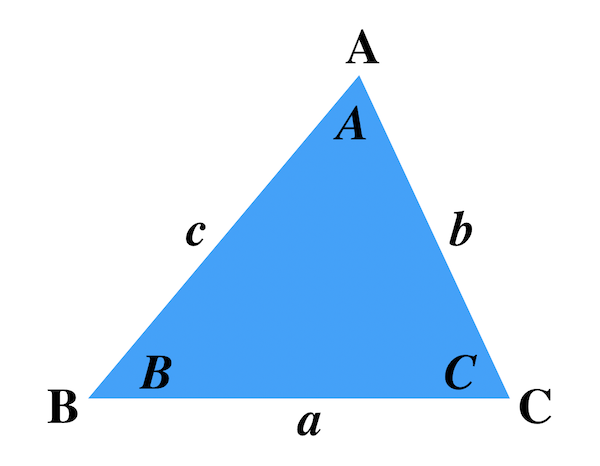
三角形の辺の長さと角の大きさ、そして外接円の半径の関係をサインやコサインで表した式です。 ページトップへ戻る Step1 正弦定理と余弦定理 この記事で扱う正弦定理は三角形の 向かい合う「辺」と「角」 外接円の半径 がポイントとなる定理で,三角形を考えるときには基本的な定理です. 一連の記事はこちら 三角比1|三角比を考え方から理解する! 有名角の三角比も! 三角比2|sinθ, cosθ, tanθの超重要な4つの関係式 三角比3|実は当たり前! ? 3つの (90°θ)型の変換公式 三角比4|角度が90°以
Incoming Term: 三角形の比の定理 ポイント,
コメント
コメントを投稿