【人気ダウンロード!】 ��角形の比の定理 中学 176418-三角形の比の定理 中学

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト
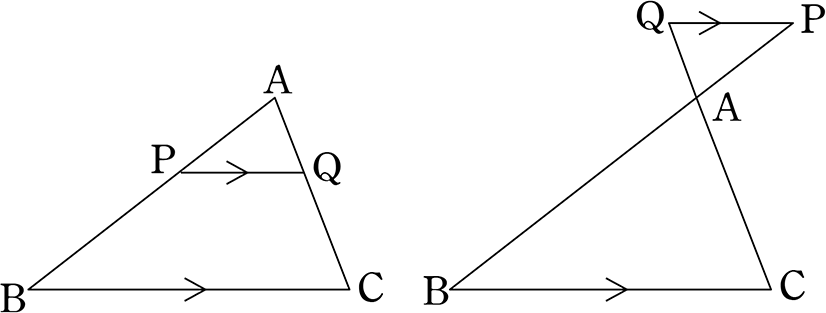
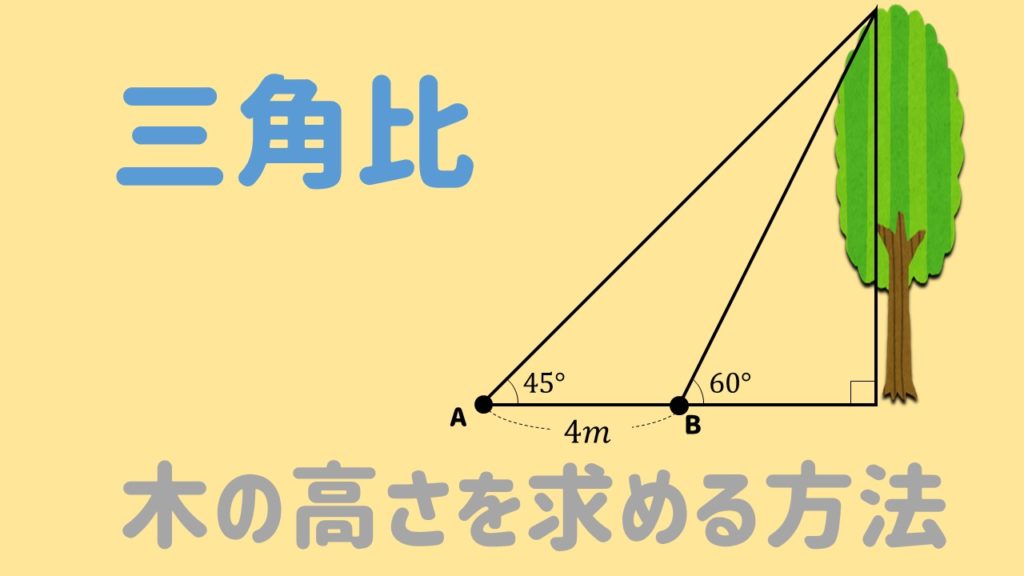
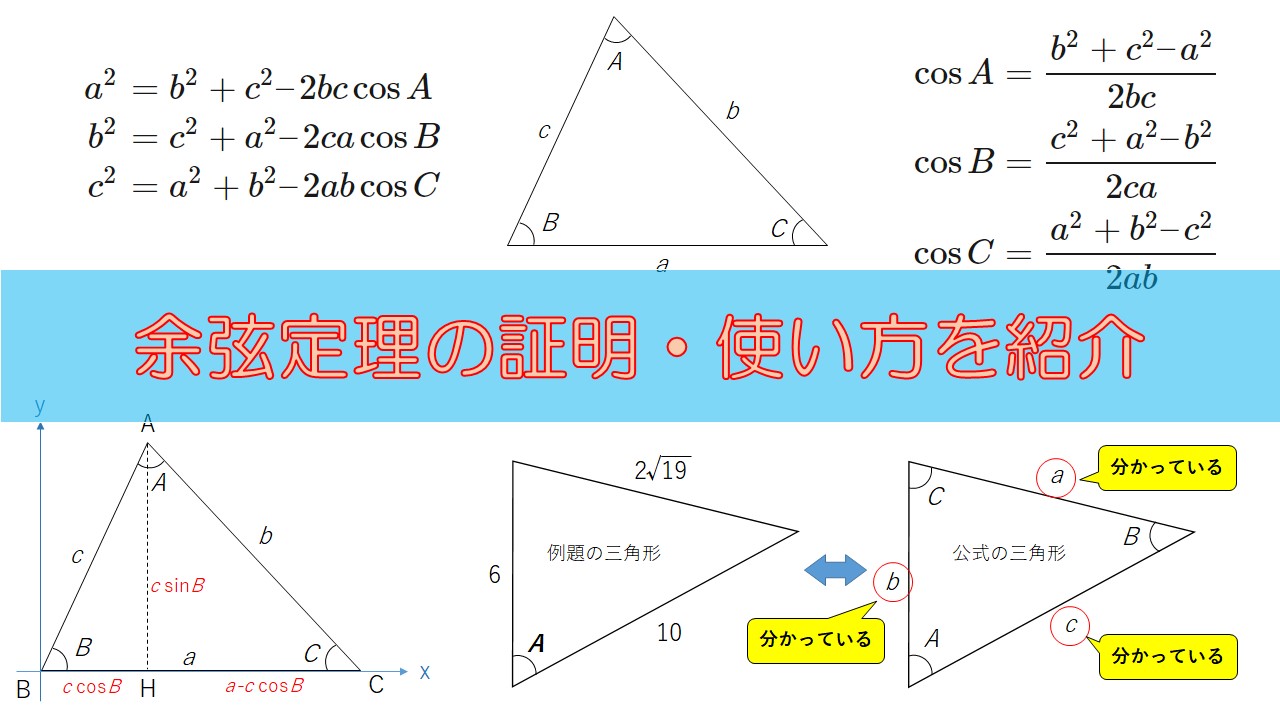
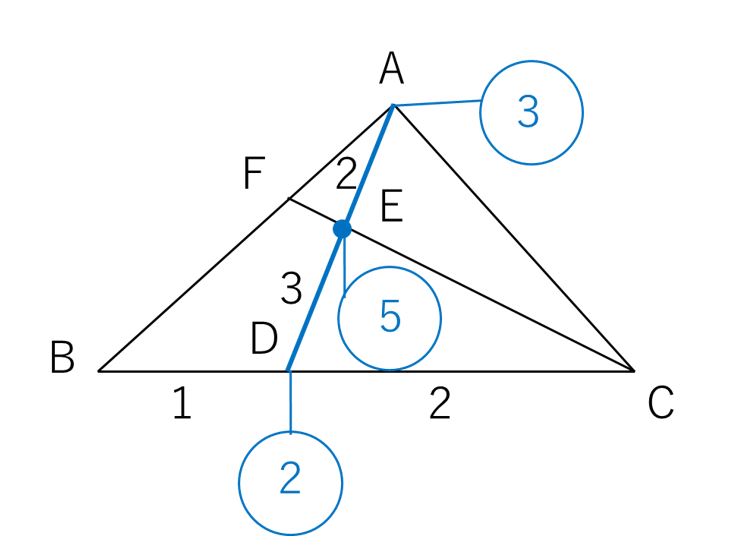
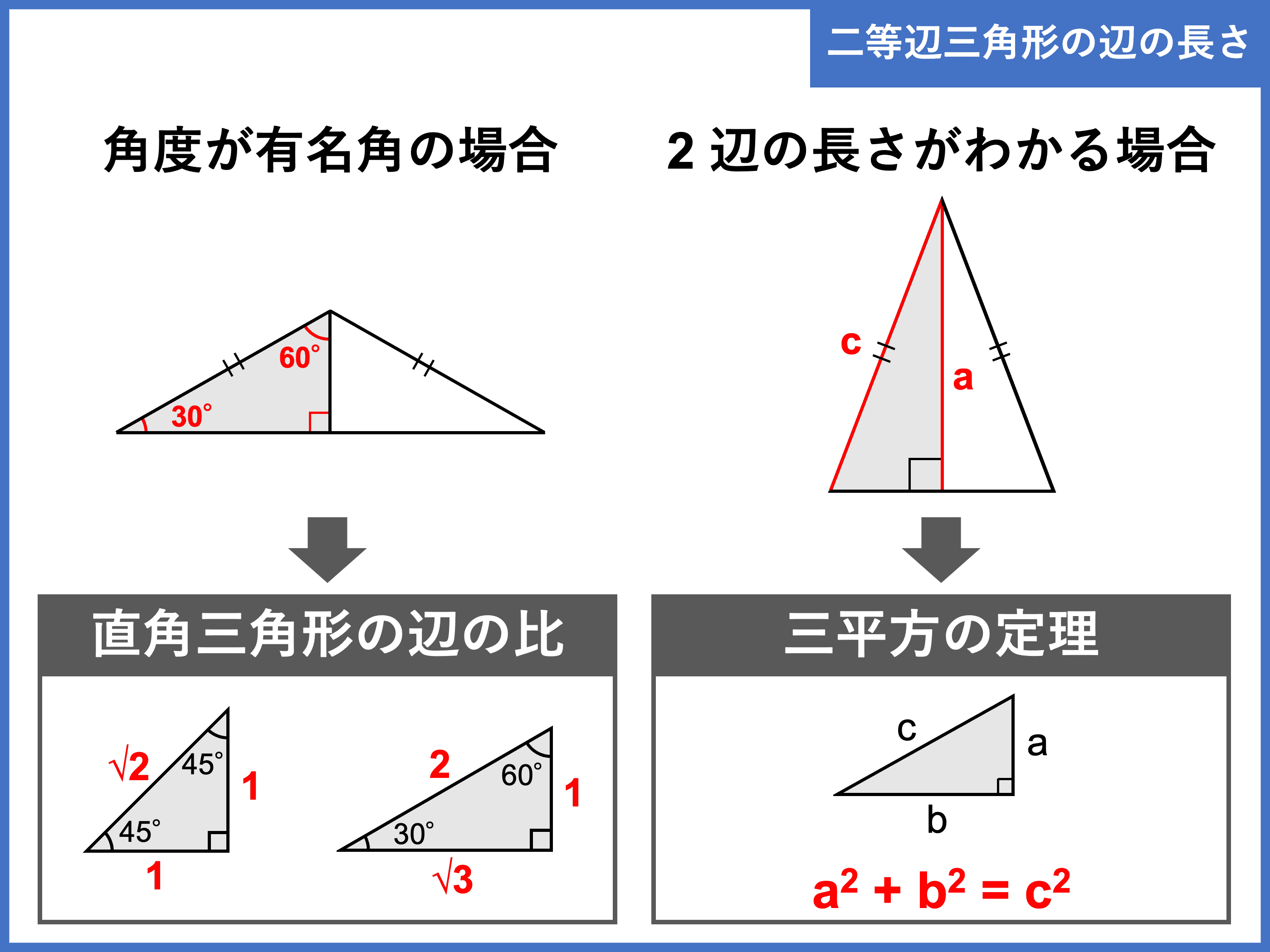
直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の 直角三角形 45°,45°,90°の 直角三角形 3辺の比は となります。 3辺の比は知っておくと役に立つ以下の定理があります。 角の 2 2 等分と線分の比 下図のように、角 A A の 2 2 等分線と、 BC B C の交点を D D とします。 このとき、 BD DC = AB AC B D D C = A B A C 一応、中学数学の範囲外なので、頻繁に出題されるものではありませんが
三角形の比の定理 中学
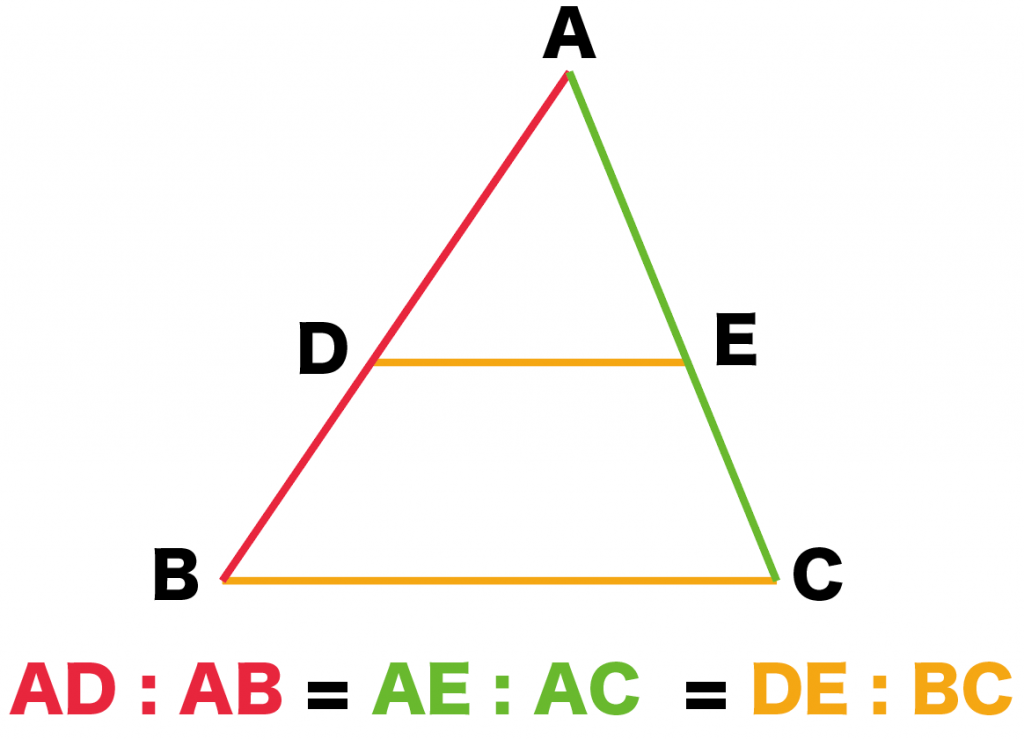
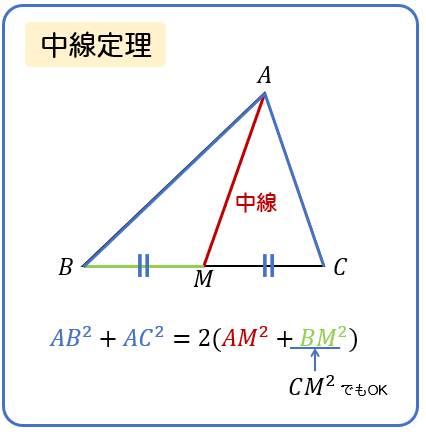
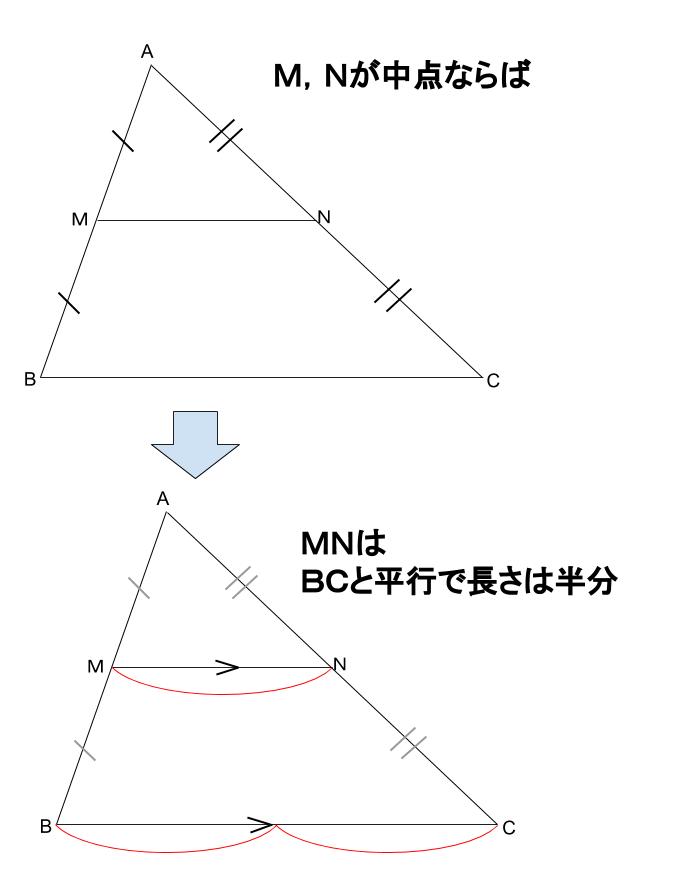
三角形の比の定理 中学- 中点連結定理 三角形の2辺の中点を結ぶ線分は、残りの辺に平行で、長さはその半分である 三平方の定理 ピタゴラスの定理 直角三角形の直角をはさむ2辺の長さをa,b、斜辺の長さをcとすると、次の関係が成り立つ a 2 b 2 c 2 相似比 (表)面積の比は、nm=n 2m 2学習する学年:中学生 1.三角比って何? 三角比とは、直角三角形の3つある角の90度以外のどちらか1つの角度が決まれば、3つの辺の長さの比率が決まるという性質のことです。 注意:直角二等辺三角形の場合は角度が決まらなくても3辺の比率は決まってしまいます。
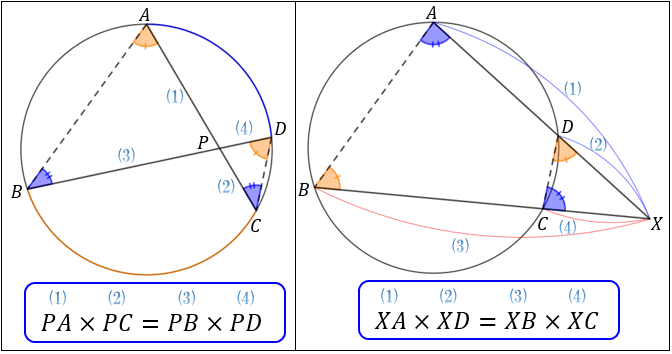
中学生ができるトレミーの定理の証明方法
中学数学公式一覧 Ver112 (21 年5 324 三平方の定理 直角三角形の 斜辺の2 乗は、その他2 辺の2 乗の和になる a2 b2 = c2 A B a C b c 325 ピタゴラス数 a2 b2 = c2 を満たす正の整数の組(a,b,c) のことを、 ピタゴラス数と呼ぶ ピタゴラス数は無限個存在する (a,b,c) = (3,4,5),(5,12,13),(7,24,25),(8,15,17),··326三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon)は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。 三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に
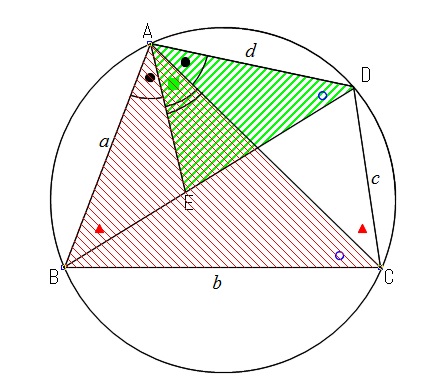
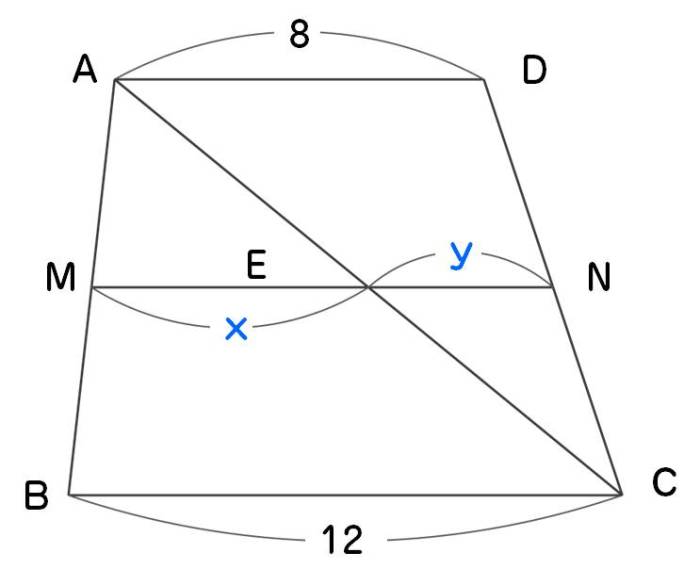
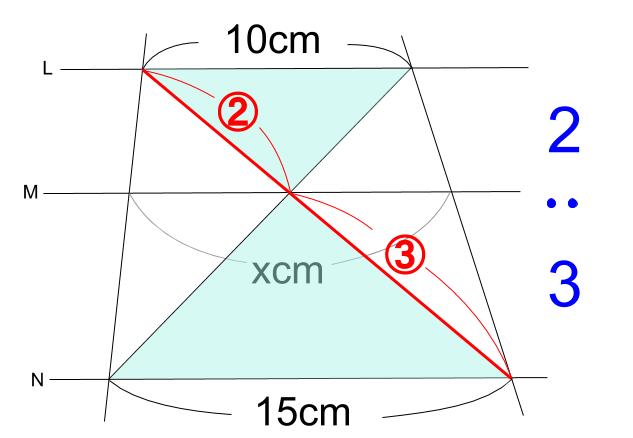
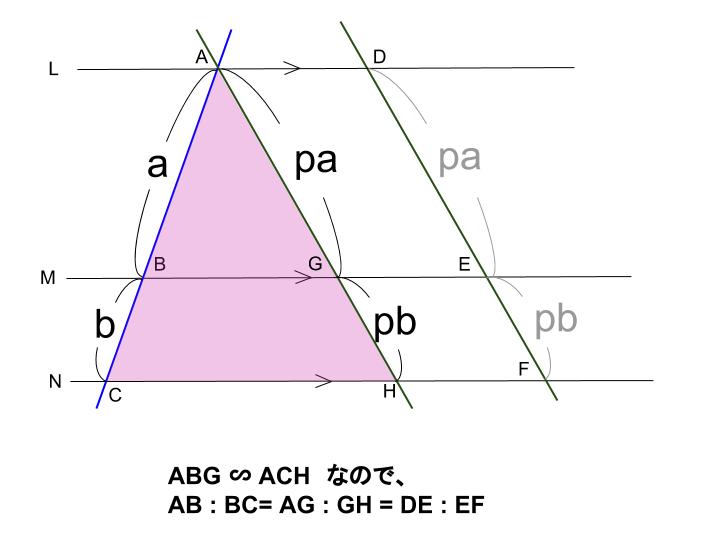
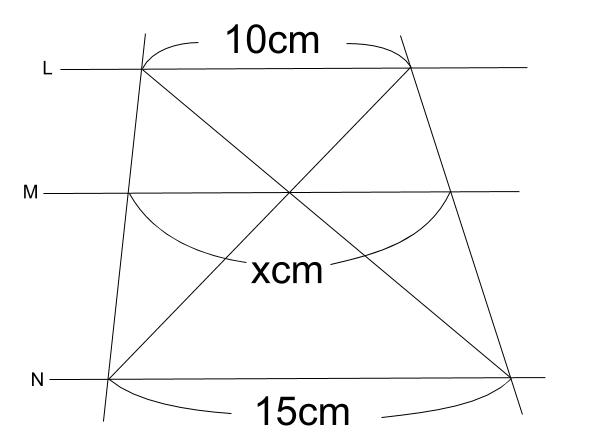
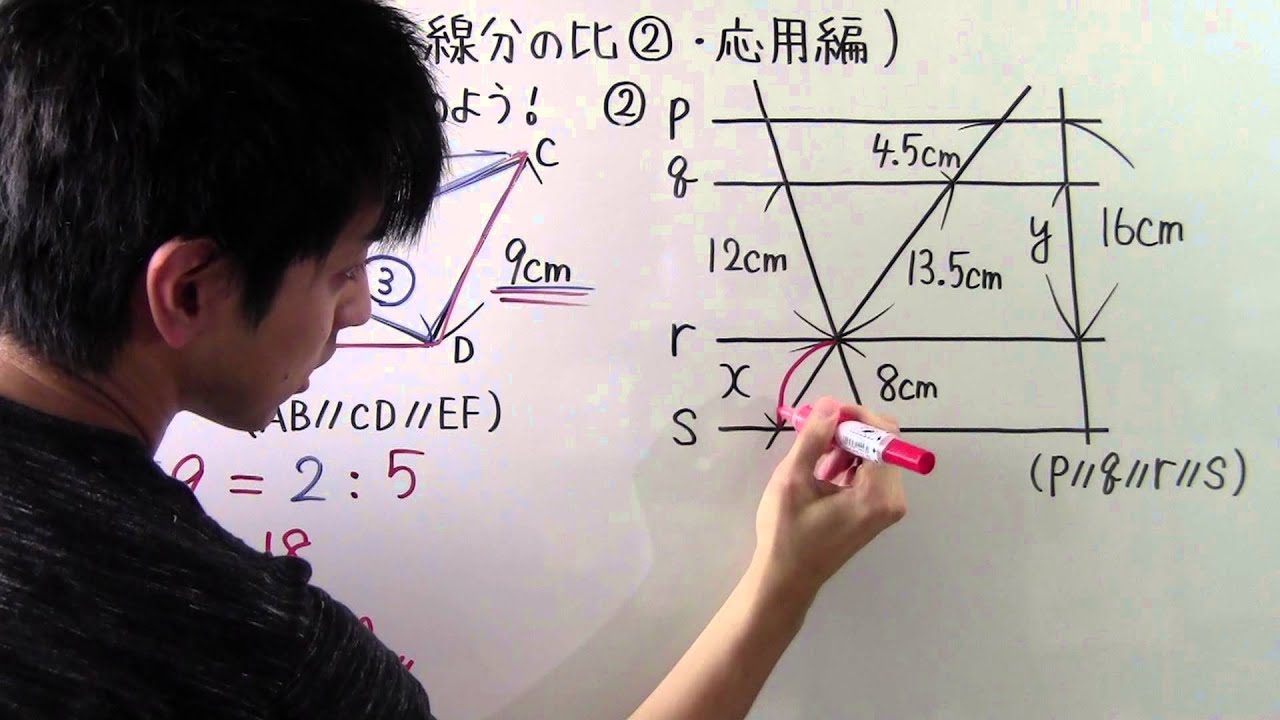
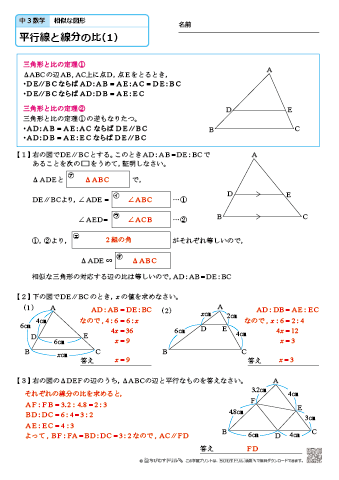
次の3つの条件のうちどれか1つが成り立てば、2つの三角形は相似の関係です。 ・3組の辺の比がすべて等しい。 ・2組の辺の比が等しく、その間の角が等しい。 ・2組の角がそれぞれ等しい。 画像のの問題の場合、 「2組の辺の比が等しく、その間の角が等しい。」 に当てはまります。 adeと abcで、 対応する2組の辺の比が等しいことを ⑴では、 「adab=aeac」 と チェバの定理の逆もどうぞ平面図形 中学数学 高校数学 チェバの定理が使える図形とは 数学おじさん まずは、チェバの定理が使える図形だ!と気づかなければ始まらないんじゃな こんな図形のときに、チェバの定理が使えるんじゃな 具体的に言うと、 三角形が対象; 緑に対して「平行線と線分の比の定理①」を用いると、 6 x = 8 12 ① 6 x = 8 12 ① オレンジに対して「三角形と比の定理②」を用いると、 8 ( 8 12) = 4 y ② 8 ( 8 12) = 4 y ② ①を整理すると、 6 x = 2 3 6 x = 2 3 比例式は「内積の項 = 外積の項」が成り立つので、 2 x = 18 2 x = 18 よって、 x = 9 x = 9 ②を整理すると、 2 5 = 4 y 2 5 = 4 y
三角形の比の定理 中学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形の比の定理 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 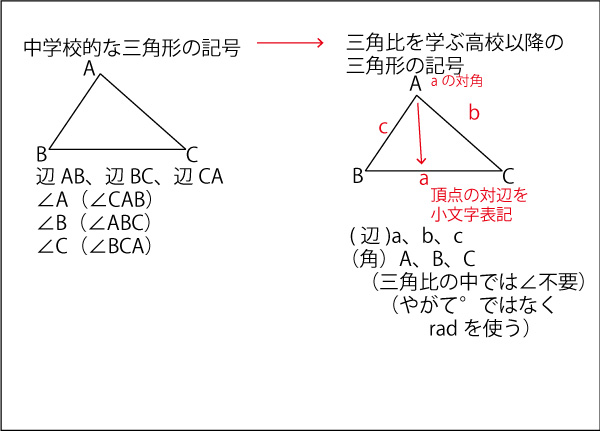 |
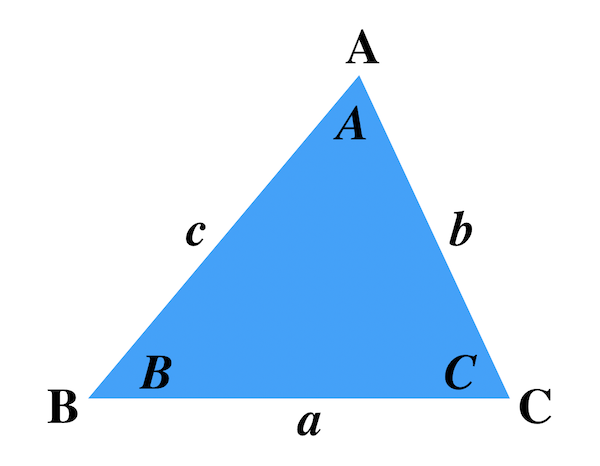
ここでは、三角比の関係式から、三角形の形状を答える問題を考えます。 角度は考えづらいので、正弦定理や余弦定理を使って、三角比を辺による表現に変えて考えていきます。 なお、 AB = c A B = c, BC = a B C = a, CA = b C A = b と書き、角の大きさは ∠CAB = A ∠ C A B = A, ∠ABC = B ∠ A B C = B, ∠BCA = C ∠ B C A = C と書くことにします。 目次 例題1 例題2 おわりに 広告 ※ S 3 = c 2 大きな正方形 S 1 は、三角形 S 2 4つと 真ん中の正方形 S 3 との合計でも求めることが出来ます。 S 1 = 4 S 2 S 3 ( a b) 2 = 4 × a b 2 c 2 a 2 2 a b b 2 = 2 a b c 2 ∴ a 2 b 2 = c 2 よって、ピタゴラゴラスの定理 a 2 b 2 = c 2 が導き出されました。
Incoming Term: 三角形の比の定理 中学,
コメント
コメントを投稿